Ez a jegyzet nem "kötelező tanagyag",  a számítógépet e nélkül a tudás nélkül is használhatja bárki, de nem árthat, ha egy kicsit a dolgok mögé látunk. :)

Az iskolában megtanították mindannyiunknak a tízes számrendszert. Ebben ugye tíz számjegy van, 0-9 vannak a számok. Nullával kezdődik és a számrendszer nevénél eggyel kisebb a legnagyobb szám. A tízes számrendszerben helyiértéket pedig ugye jobbról balra úgy tanultuk, hogy egyes (ez 10 a nulladik hatványon=1), tízes (10 az első hatványon=10), százas (10 a másodikon=100), ezres (10 a harmadikon=1000), stb.  

A számítógép kettes számrendszerben dolgozik.

Miért nem volt jó neki a tízes? Azért, mert az adatokat a meghajtón mágneses* információként tárolja: mágnesezve van=1, nincs mágnesezve=0. Ez a számítógépes adattárolás legkisebb egysége a bit. Jele a kis b betű. Az informatika hőskorában kiszámolták, hogy 256 karakteren mindent** meg tudnak jeleníteni. Kiosztották, hogy az első 128 karakter a mindenki által használt betűkre, jelekre (ékezet nélküli betűk, számjegyek) a második 128 jelet pedig adott nyelvek a saját betűformáira igazíthatták.
A Közép-Európaiban például ott vannak a mi ékezetes jeleink, de megtalálható másik betűtípusokban a spanyolok, vagy más nemzetek speciális lejjelei is.

A lényeg, hogy 256 adat tárolását kellett megoldani a kettes számrendszerben.
Ezt 8 helyiértéken sikerült megcsinálni:

2 a nulladik hatványon = 1 _ /minden számnak 1/

2 az első hatványon = 2

2 a második hatványon = 4

2 a harmadik hatványon = 8

2 a negyedik hatványon = 16

2 az ötödik hatványon = 32

2 a hatodik hatványon = 64

2 a hetedik hatványon = 128

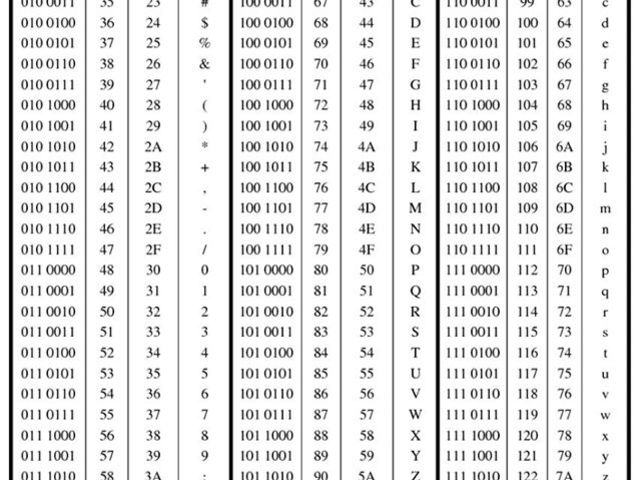
Készítettek egy táblázatot, megszámozták a tízes számrendszer szerint, és amikor a gépen rögzítjük automatikusan a kettes számrendszer szerint tárolódnak az információk.

Leütjük az a betűt, hogyan tárolódik el ez a számítógépben. Nézzük a kódtáblázatot:

Tízes számrendszerbeli kódja 97, tehát

0 db 128 van benne,

1 db 64 van benne (97-64=33), tehát maradt 33,

1 db 32 van benne, maradt 1,

0 db 16 van a maradékban,

0 db 8 van a maradékban,

0 db 4 van a maradék 1-ben,

0 db 2 van a maradékban,

1 db egyes van a maradékban.
A 97 decimális (tízes számrendszerbeli) szám bináris (kettes számrendszerbeli) megfelelője tehát 8 biten: 01100001

Ez így nekünk hosszadalmasnak és bonyolultnak tűnik, de mivel a gép csak két féle adattartalmat tud megkülönböztetni (van infó, vagy nincs, tehát 1, vagy 0) neki így egyszerűbb. Ezen kívül az ő műveleti végrehajtási sebessége összehasonlíthatatlanul gyorsabb, mint az emberi agy.

Erről egy apró kis történet:
A kilencvenes évek elején szerettem volna hasznossá tenni magamat, és felajánlottam a bérelszámolás csoportvezetőjének, hogy használják azt a kis programocskát, amit a címletezésre írtam. Ez ugye arról szól, hogy a sok ember fizetését olyan címletekben hozzák ki a bankból, hogy abból a legoptimálisabban ki lehessen fizetni az embereket. Erre ezt a választ kaptam:
- Köszönjük, de Marika néni sokkal gyorsabban el tudja ezt a munkát végezni, mint a számítógép.

Azóta is furcsálom, hogy Marika nénit nem állították még ki világ csodájára. :)

Az informatikában alkalmazzák még a nyolcas (octo), és a tizenhatos (hexa) számrendszereket is, de erről most itt nem írok. Ha másért nem, hát azért sem, mert nem szeretném, ha a nyájas olvasó kiszaladna a világból. :)  (Akit érdekel a technikája: ráhúzható arra is a tízes és a kettes számrendszer 'kaptafája' /nullával kezdődik és a számrendszer nevénél eggyel kisebb a legnagyobb szám/, no de erről tényleg nem írok többet.)

____________

* - a CD és DVD lemezen nem mágnesen módon tárolják az adatokat, hanem speciális módon vannak kialakítva (égetve, préselve), de a lényeg ott is az, hogy van jel, vagy nincs jel.

** - a kínai és japán nyelvben ezt nem tudom hogyan oldották meg, mert ott sokkal több a jel és a karakter, de ez legyen az ő gondjuk. :)